Sports Promotions

@Ben Marrow

A friend recently alerted me to this promotion:

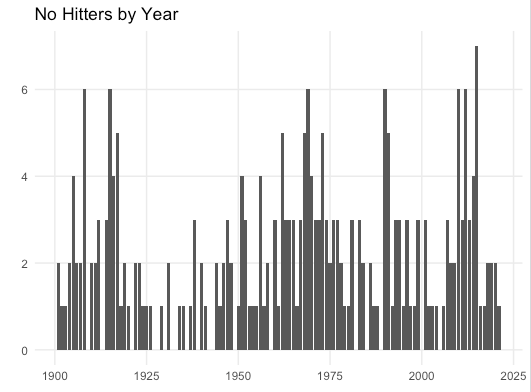
Is this a profitable venture? Probably. No hitters are pretty rare — only 306 in total since 1876, 251 since 1901, and none for the Red Sox since 2008. It doesn't help that the Red Sox are pitching worse than average this season in WHIP and ERA.

More specifically, let's say there's a $p\%$ chance that a no-hitter is thrown in a season and that Jordan's Furniture has gross margin of $\alpha$. Then, if the promotion increases sales by $X\%$, the promotion is profitable if and only if

The first term gives the costs to Jordan's if a no-hitter is pitched, reflecting the fact that Jordan's only incurs the cost-of-goods-sold and not the sale price. The second term reflects the gross profits to Jordan's if a no-hitter is pitched, in which case Jordan realizes its full gross margin per dollar.

If this year's Red Sox reflect the average pitching ability of the MLB, then a generous guess for $p$ is 1%. (The unconditional probability of a no-hitter in a game is 0.12%; the average percent of no-hitters per season is 0.15%). Since Jordan's isn't publicly traded, we can't observe its margins, but let's assume it had the same gross margins as Wayfair did in 2020, roughly 29%. Then the multiplier from the promotion is:

So for every $X$% increase in sales, expected net income goes up $0.28\cdot X\%$. (Intuitively, this basically says that Jordan's earns its gross margin with near certainty). Jordan's had 279.4M in revenue last year, so a 1% increase in sales due to this promotion could plausibly net the company (in expectation) +$780,000. Even if the probability of a no-hitter jumped to 10%, the expected net income would still be +$530,000.

In fact, in this simplified model, the promotion is always profitable as long as the gross margin exceeds the probability of no-hitter. So under the Wayfair margin assumption, the probability of a no-hitter would have to jump to 29% to make the offer unprofitable. Alternatively, Jordan's could expect to breakeven just by promising the full rebate if Alex Verdugo (career BA = 0.285) gets a hit on any given at-bat.

Free Chick-Fil-A

Speaking of sports-contingent freebies, I'm reminded of a stadium promotion that the Houston Rockets once did (and perhaps still do?) in partnership with Chick-Fil-A.

If an opposing player “misses two consecutive 'fowl' shots” during the 4th quarter of a Rockets home game, fans at Toyota Center can redeem their tickets for a free Classic Chicken Sandwich.

(To clarify, the misses have to be consecutive within the same play).

Fortunately, in the one Rockets game I attended on December 31, 2019, Mason Plumlee missed his two free throws at the beginning of the fourth quarter, covering my first lunch of the new year. It also made me wonder how frequently this promotion paid out.

Scraping play-by-play free throw data takes a long time to do, so I'm only going to present the results from 2018-2019. In that season, there were 55,952 free throw attempts, 76.6% of which were successful:

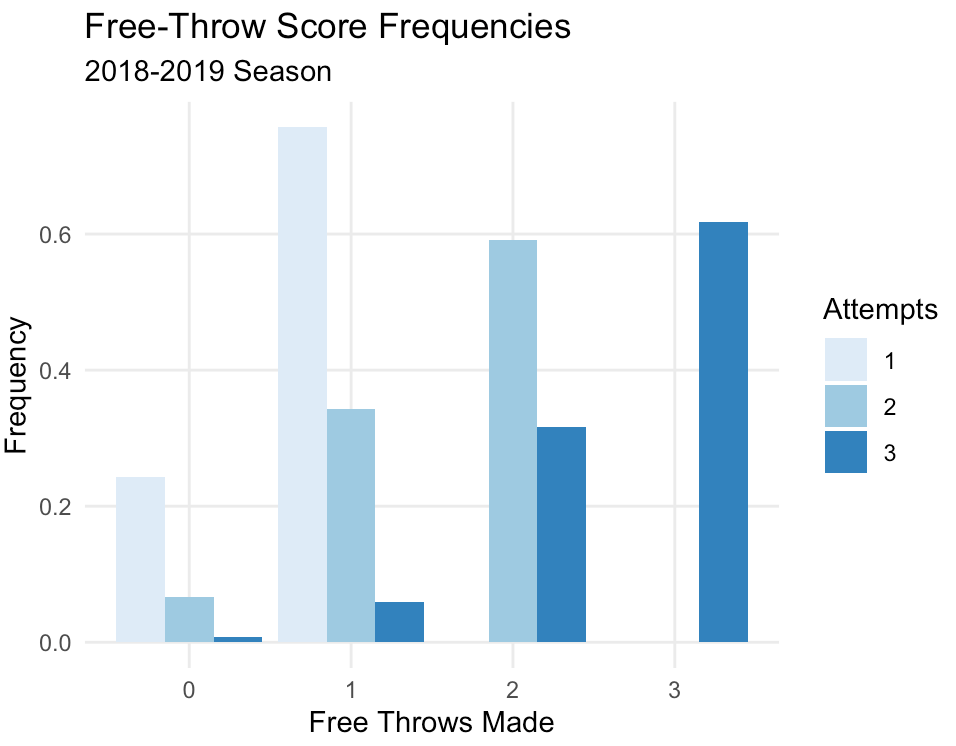
If $p=0.766$ is our binomial sufficient statistic, then what's the probability that 2 in a row are missed? On 2-point free throw attempts, its $(1-0.766)^2=5.4\%$. On 3-point free throw attempts, missing 2 consecutive free throws can occur in three ways $\{(0,0,1),(1,0,0),(0,0,0)\}$, so the probability is $2(1-0.766)^2(0.766)+(1-0.766)^3=9.67\%$. Since 2-point free throw attempts are 24 times more frequent that 3-point free throw attempts, our estimated probability on any given play is

Of course, there are obvious adjustments one may make for differences in fourth quarter fouls, away team shooting, streak-contingent accuracy, etc. The effects of these are not always obvious. For example, we usually think of away teams as playing with a disadvantage, but if anything, the away team seems less likely to miss on two-point free throws.

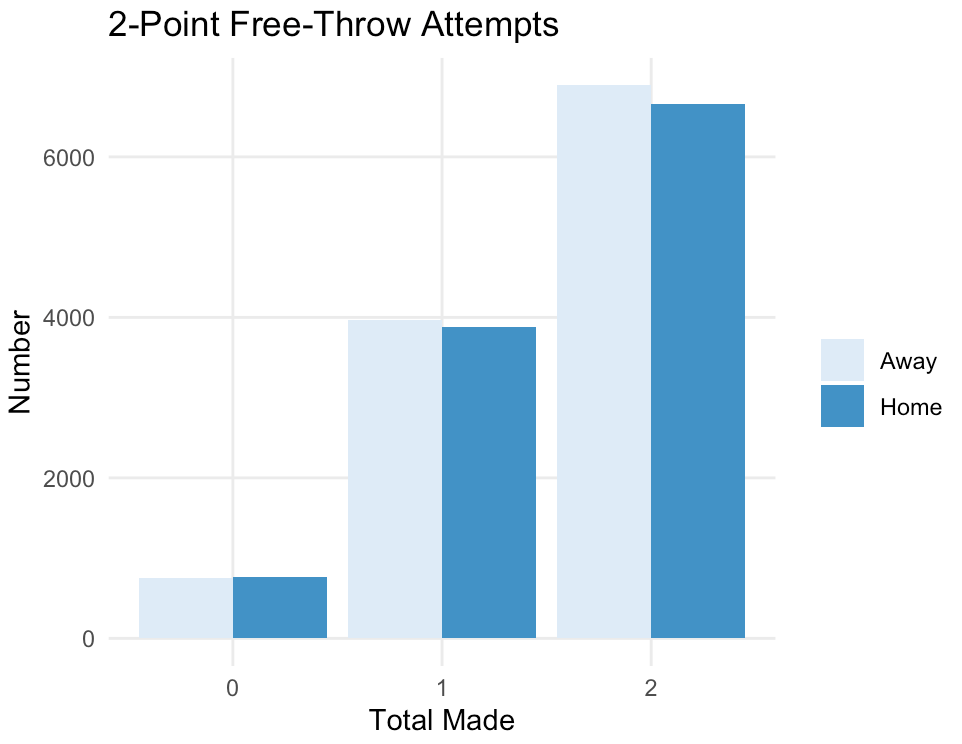
Not surprisingly, the fourth quarter typically has more 2 and 3 point free throw attempts than any of the other quarters. The average fourth quarter in 2018-2019 saw 5.77 free-throw plays, of which 3.16 went to the away team. Using the numbers above, that gives an $\approx$16% chance that any given game has the opposing team miss two free throws in a row in the fourth quarter.

And this is basically what we observe. Among eligible plays, (2 or 3 point free throws in the fourth quarter by the away team), a consecutive miss was observed in 6.2% of plays. Unconditionally, an away-team player missed two free throws in the fourth quarter in an astonishing 19.1% of games! Maybe Chick-fil-a wasn't so smart to offer this promotion after all.