Predictability in Sabermetrics
@Ben Marrow
What makes a sports statistic a "good" statistic? One simple answer: a statistic is good insofar as it correlates with the objective of a given sport — wins for a pitcher, points-per-game for a basketball player, assists for a hockey player, etc. In this regard, the goal of sports statistics is an exercise in dimensionality reduction to find the best predictors of wins.
Another view is that statistics are heuristics to measure the latent ability of a player. According to this view, an athlete has some true level of unobserved ability, and the observed data are noisy measures of this ability. The purpose of sports statistics is then to combine the data appropriately to filter out the noise.
Though they may appear similar (what is "ability" if not the capacity to produce wins?) these views have different implications for the appropriate criteria used to evaluate good statistics. One reason is that most people tend to believe that latent ability is a fairly sticky quality: though the ability of an athlete will vary to some degree season over season, and may trend down (or up) with age, if our measure of ability varies wildly season over season, it seems more likely that our measure of ability is flawed than that ability as a trait is highly variable.
I recently learned that earned run average (ERA), one of the most — if not the most — commonly used pitching statistics, demonstrates a comparatively low year-on-year autocorrelation of roughly 21%. In other words, variation in league-wide ERAs one season tells us surprisingly little about variation in league-wide ERAs the subsequent season.
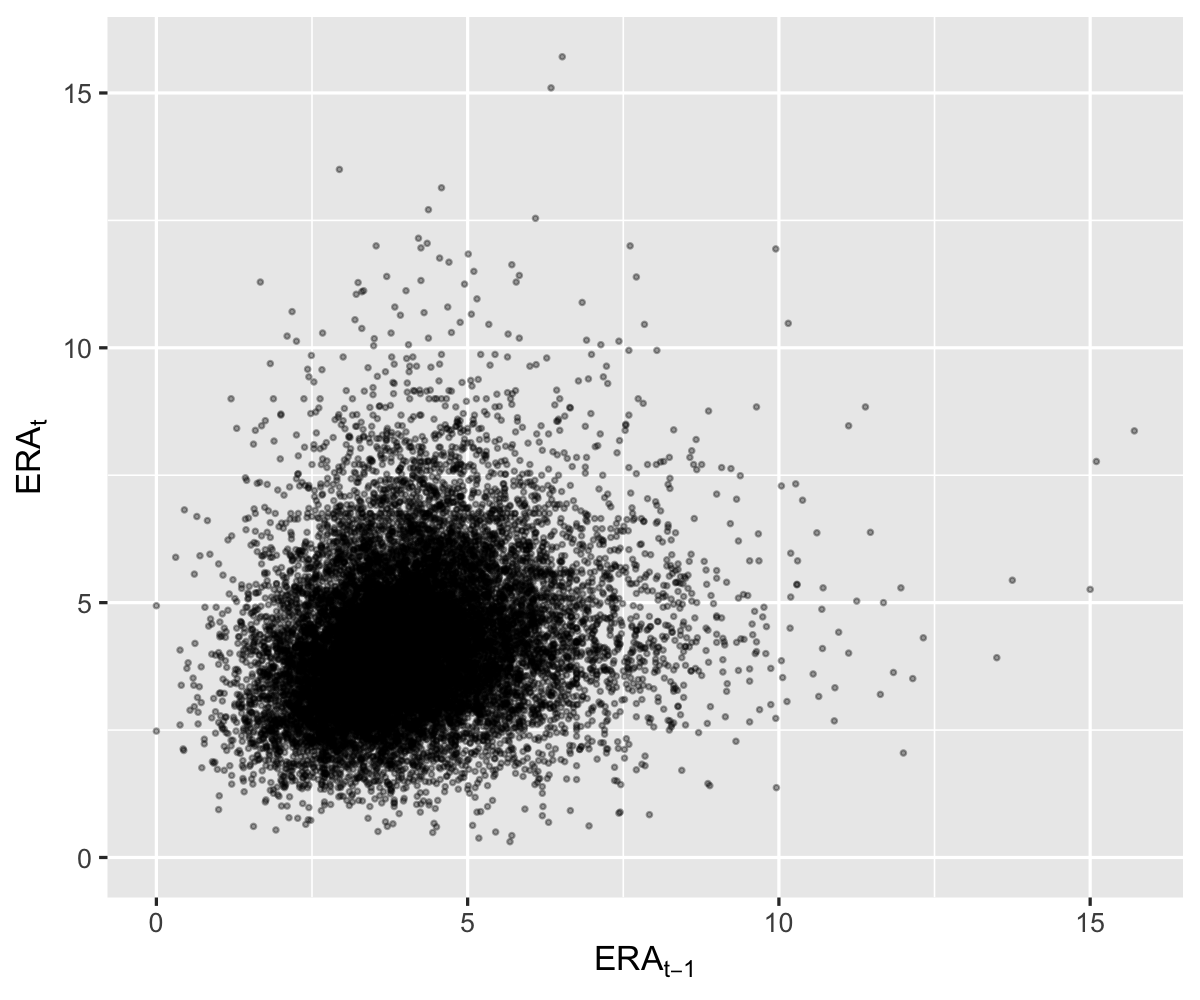
As I also learned, this is apparently a well known critique of ERA, which is why many analysts opt instead to use Fielding Independent Pitching (FIP). Unlike ERA, FIP "focuses solely on the events a pitcher has the most control over -- strikeouts, unintentional walks, hit-by-pitches and home runs. It entirely removes results on balls hit into the field of play." The idea here is that balls in play — which rely on fielding ability, quasi-random placement of the ball, runners on base, etc. — contribute noise to the measure of pitchers' ability in a way that walks, strikeouts, and homeruns do not.
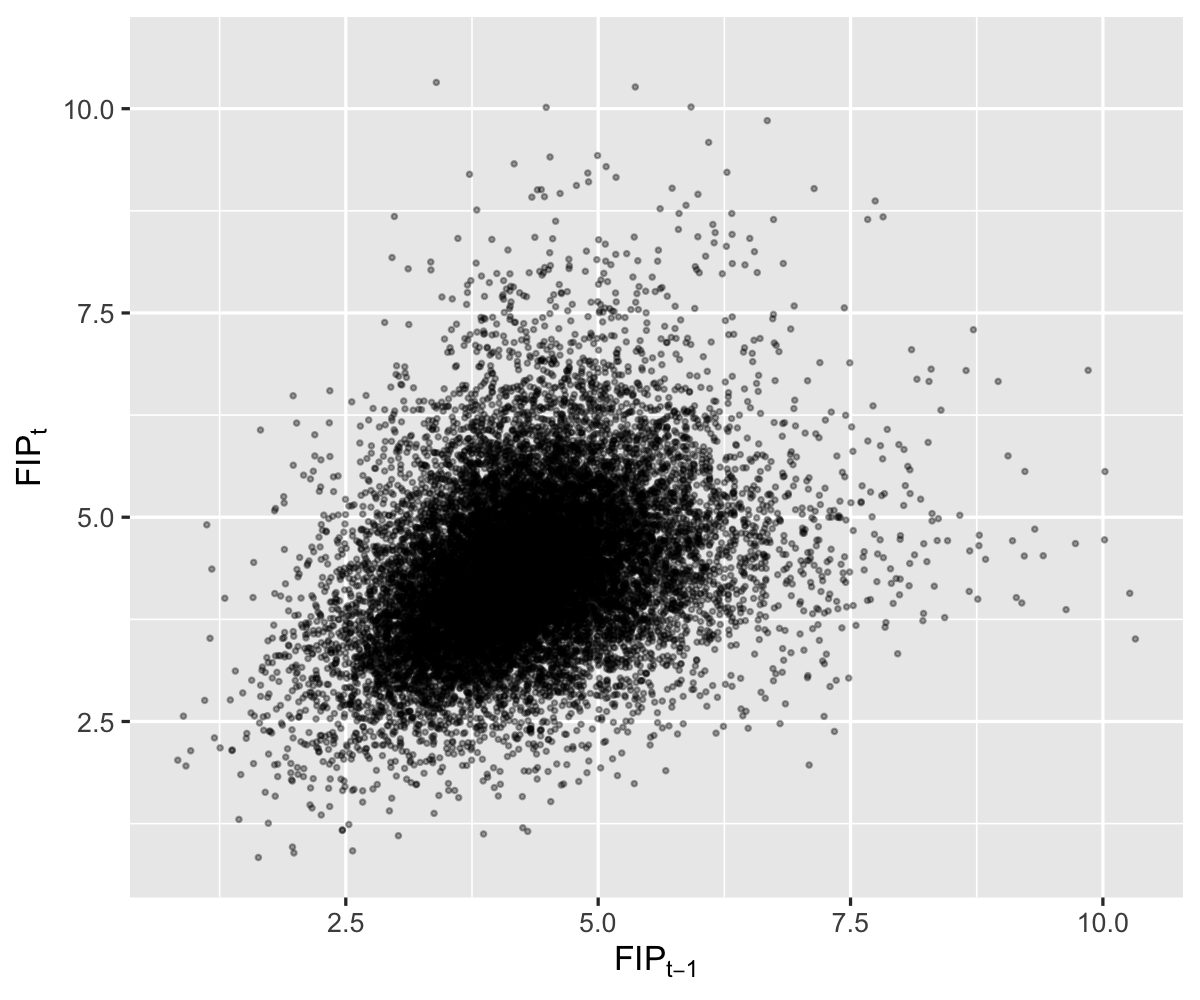
Hence I was also surprised to see that while an improvement over ERA, FIP also has a relatively low YoY autocorrelation of 35%.:
Lest one worry that pitching ability is inescapably noisy, many other measures of pitching ability demonstrated quite large year-on-year predictability. Strikeout-rate — defined as number of strikeouts per inning pitched — displayed a remarkable 81% autocorrelation, followed by walk rate (52%), home run rate (45%), and hit rate (30%).
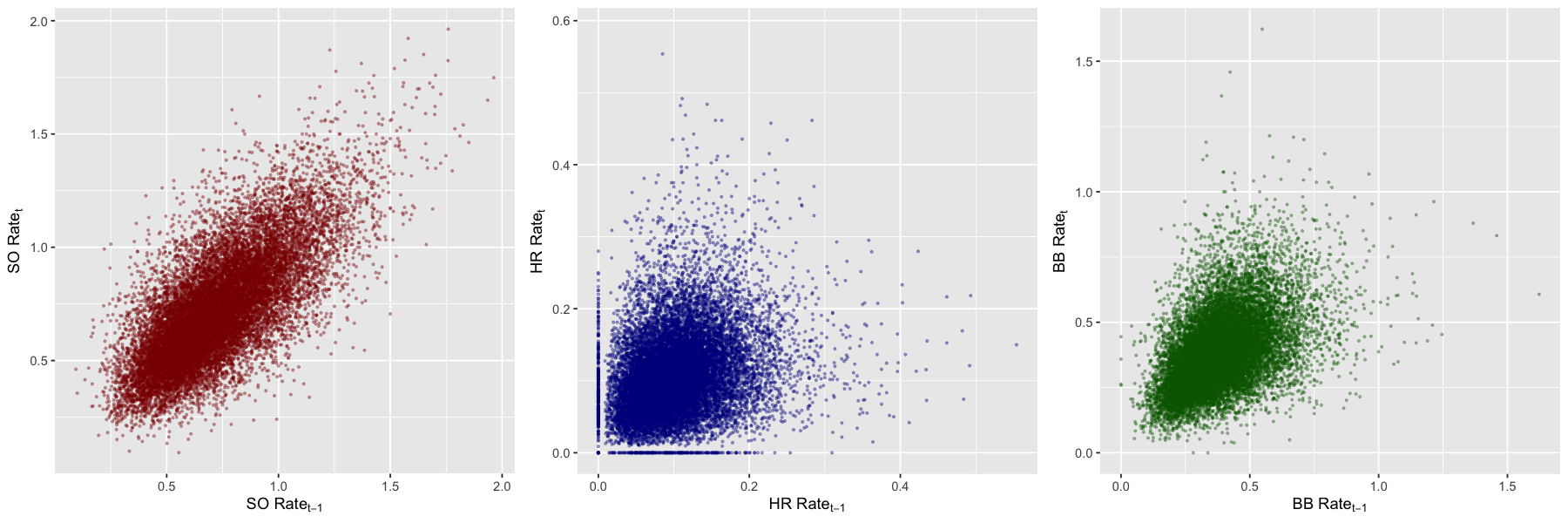
Moreover, and with the slight exception of walks, these autocorrelations are fairly stable over time.
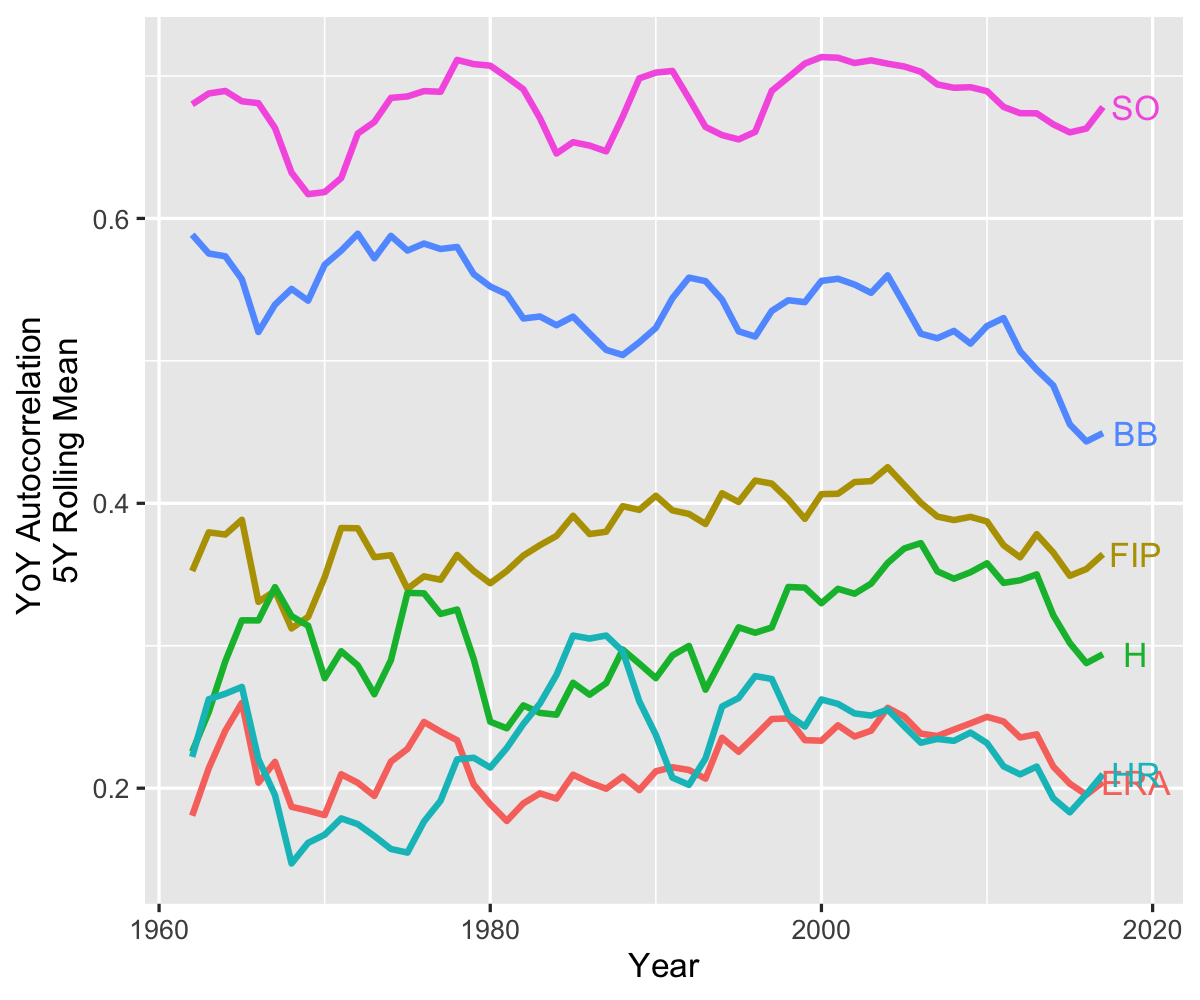
The curious issue at play is that individual measures associated with pitching ability — strikeouts, walks, etc — can have quite large autocorrelations, while the very act of combining them into a summary statistic decreases autocorrelation. This is perhaps surprising because we tend to think of combined statistics as a way to filter out noise and increase predictability. One intuition might be as follows: imagine that the strikeout rate is strongly associated with a pitcher's tendency to throw outside the strike zone, but not with his ability as a pitcher overall (in particular, this pitcher would also have a high walk rate). Then autocorrelations in the constituent characteristics can be high while some combined measure of walks and strikeouts is less predictable year-over-year.
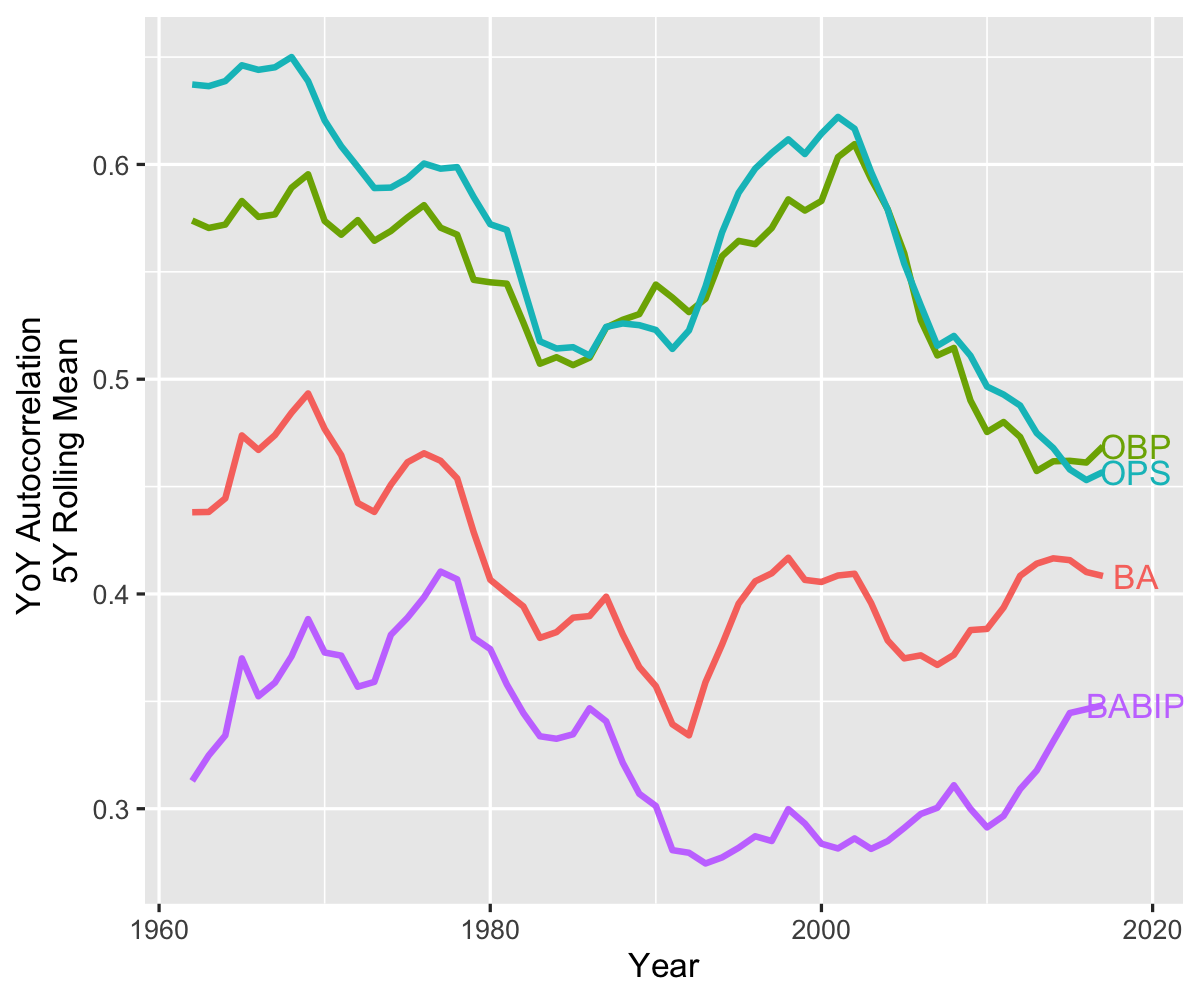
There are somewhat similar dynamics at play with such batting statistics as on-base-percentage (OBP), on-base plus slugging (OPS), batting average (BA), and batting-average on balls in play (BABIP). Given that, conditional on a ball being in play, whether or not its a hit is fairly random, the low autocorrelation of BABIP is not surprising. What is interesting is the fairly sudden drop in autocorrelations for OBP/OPS since the turn of the century.