A Question about Options Trading

@Ben Marrow

June 19, 2020

First, a motivating question: suppose you knew for a fact that company XYZ, currently trading at $90 per share, will rise to $100 in the next week. (Perhaps you have a strong prior that the new product will be a success, or you came across some material non-public information; the important caveat is that the rest of the market does not know).

What options position should you take to maximize your profits?

The standard objects of interest in options trading are the so-called "greeks", mathematical objects that give the change in the price of an option corresponding to changes in some underlying features of the security. Formally, they give partial derivatives of option value with respect to other parameters. The main three ("first order greeks'') are delta, vega, and theta, which tell how the value of an option changes with (respectively) the price of the underlying stock, the volatility of the underlying stock, and the time until expiration.

Clearly, very in-the-money options have a very high delta, since a $1 increase in the underlying stock will almost certainly translate into $1 additional option value. So one way to take a position would be to purchase a very in-the-money option on XYZ, say at a strike of $2. With a delta close to 1, each option would net ~$10 in profit in the next week.

But investors don't care about absolute profits, they care about returns. The delta of an option gives

\Delta =\frac{\partial V}{\partial S}

Where $V$ is the value of an option and $S$ the value of the underlying stock. Investors presumably care about

\frac{\partial V/V}{\partial S/S} = \Delta \frac{S}{V}

I assume this latter quantity would be the basic object of interest to any options trader: it quite literally gives the elasticity of option price with respect to the stock price. But a cursory online search returned very little. Wikipedia described the object in question as Lambda (with no additional description). Investopedia also described the object as Lambda but then in a separate article described the very same quantity as Omega. Standard textbooks like Cochrane's Asset Pricing and Steve Shreve's Stochastic Calculus for Finance had no mention of this object at all.

Nor was the answer intuitive. Very in-the-money options have a high delta, but high $V$ (high cost of purchasing the option). Very out-of-the-money options have a small delta but are cheap.

Black-Scholes, the textbook model of options pricing, gave one possible answer. Figure 1 below illustrates in the top panel, how both the cost and the delta of an option are increasing as the stock becomes more in-the-money. The second panel illustrates our object of interest, Lambda. The monotonic decrease suggests that the largest returns come from the most out-of-the-money options. In other words, an investor would maximize profits by buying the highest strike available.

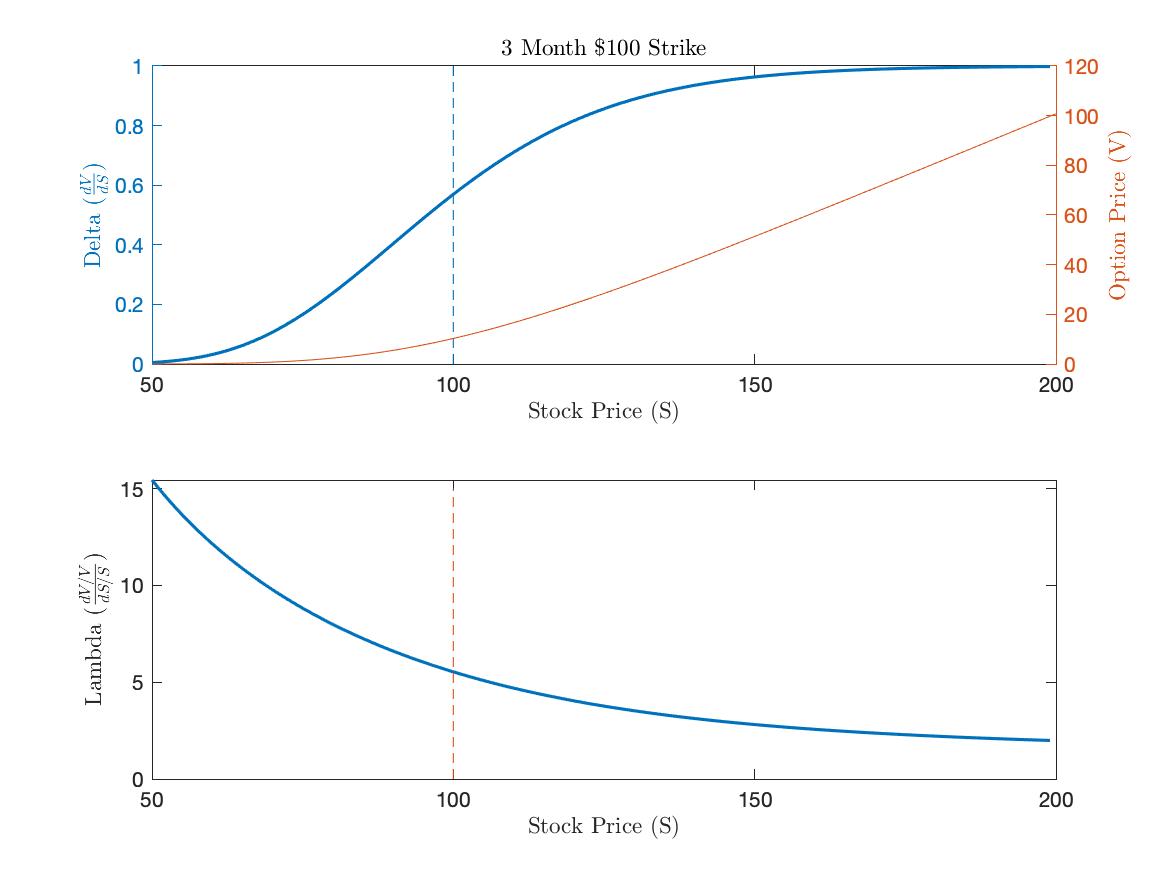
Figure 1: Lambda and Delta vs. Stock Prices

Figure 2 makes this notion more precise by looking at the returns for our hypothetical company XYZ. A strike of 200 would net a 350% return; by contrast purchasing the at-the-money option would yield a return closer to 90%.

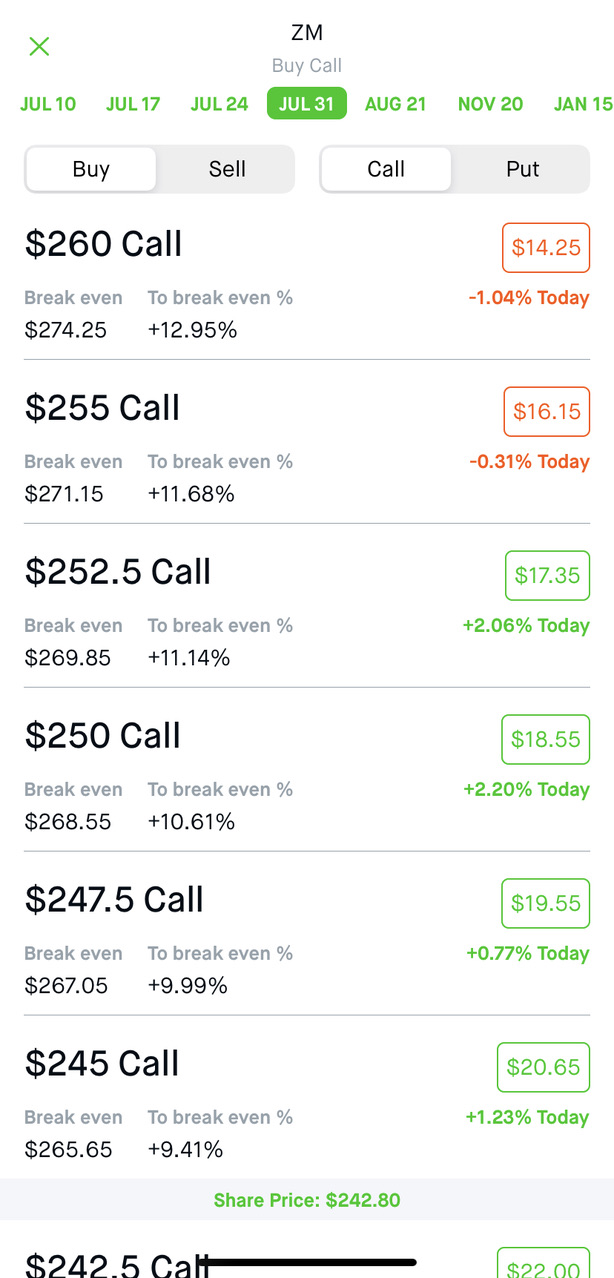
One implication of this result is that for two options on the same underlying stock with the same time until expiration, the further OTM option should always have a larger percent change in value (in either direction). But consider the daily changes on Zoom (ZM) options from June 19. Not only is the change non-monotonic as we increase the strike; some of the more OTM options actually displayed negative returns. To be sure, further OTM money options are often less liquid, as was likely the case with the zoom calls pictured below.

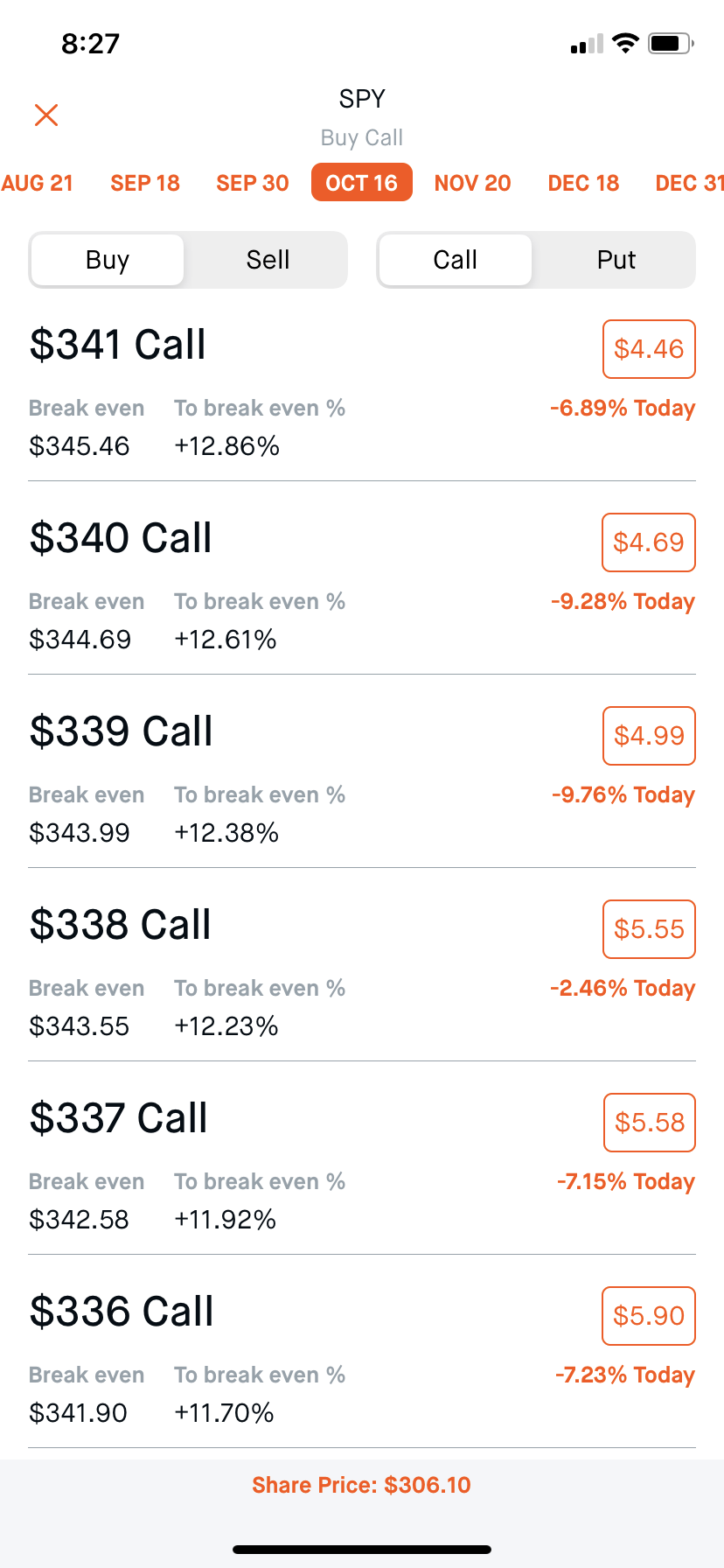
But even highly liquid options, such as those on the SPY, saw non-monotonicities across the strike structure. The percent change in daily value was -7.23% for a $336 strike, -9.76% for a $339 strike, and -6.89% for a $341 strike.

So how do we reconcile Black-Scholes with reality?

Illiquidity: Perhaps if every option was perfectly liquid, or had a large number of active traders, we would see a world more similar to Black-Scholes. I don't find this story particularly compelling, given that the asymmetry was visible in even the most liquid options.

Volatility: Most analysts will readily admit that stock prices do not follow geometric Brownian motions with constant volatility. If there were a change in volatility that increased the probability of short term increases in stock price and reduced the probability of changes in the tails, we might see behavior as we do on Robinhood.

Thinking to the future, it would be interesting to see what characteristics of options have the highest empirical lambda. One way to do this would be to regress constructed lambda on a measure of the percent out-of-the-money of the strike, controlling for time to expiration, Black-Scholes implied volatility, the degree of liquidity on the option, and characteristics of the underlying stock. Given the large increase in (presumably amateur) retail investors on Robinhood, many of whom are motivated to trade by beliefs about coming changes in stock prices, it would be instructive to see what answer they would give to the motivating question.